Systematic Characterization of Ring-Shaped Laser Beams

Measurement results are displayed in detail and in a clear manner in the software.

© Primes

We distinguish between two types of ring beams: “plateau beams” and “single-mode ring beams”, which are employed in different laser processing domains and exhibit markedly different beam characteristics. To meet the specific requirements of both beam types and their respective applications, we analyze each with tailored algorithms.

Plateau beams are predominantly utilized in welding and surface treatment processes. They are typically generated using a two-zone fiber with a core diameter of 50–100 µm and a cladding diameter of 180–400 µm. The resulting beam is a superposition of multi-mode radiation, exhibiting a stepped intensity distribution in the processing plane, depending on the power contributions from the two fiber sections. 

Single-mode ring beams are mainly employed in additive manufacturing and micro machining. Their defining characteristic is that both the core and the ring follow a Gaussian distribution in the cross-section of their intensity distribution, approaching the diffraction limit, with a defined gap between the two.

Primes Microspotmonitor for the measurement and analysis of ring beams.

© Primes

Relevant Parameters in a Single Measuring Plane

Since conventional beam definitions are inadequate for ring beams, a new set of parameters is required to accurately describe their properties. We describe the geometric features of the ring and core separately. Utilizing ISO 13694, which specifies parameters for flat-top beams, we define the following parameters for plateau beams:

• Diameter of Ring: Full width at half maximum (FWHM) of the ring structure 
• Diameter of Core: FWHM of the core region, assumed to be situated on the plateau
• Decentering: Distance between the geometric centers of the core and ring structures
• Edge Steepness: Ratio of the area within the edge of the ring to the total beam area
• Homogeneity: Intensity variation within the plateau region
• Inclination: Slope of an inclined plane fitted to the plateau structure
• Modulation: Ratio of the maximum power density in the core to that in the plateau
• Power Share Ring: Relative power contribution of the ring section
• Power Share Core: Relative power contribution of the core section
• Power Loss: Missing power, calculated as the difference between the total power of the beam and the sum of core and ring contributions.

 These parameters provide a comprehensive geometric description of the beam. Set laser parameters can be verified using power share and modulation, while the location of the sharpest imaging of the laser beam can be inferred from the edge steepness. It should be noted, that the location of the sharpest image may differ from the location of the beam waist, as discussed later. Misalignments within the optical system manifest as inclination or decentering between the core and ring structures. It is noteworthy that a donut-shaped beam (a ring with a central hole) is equivalent to a ring beam with negligible core amplitude.

For single-mode ring beams, the calculation of these parameters requires a slightly different approach. Such beams consist of a separate core and ring, each with single-mode character in radial direction. To account for this, Gaussian fits are applied to cross-sectional intensity distributions passing through the center of gravity, yielding the width and center position for both the ring and core distributions along the cross-sectional axis. This process provides the ring diameter, ring width, and core diameter. Rotated fits at various azimuthal angles enable the extraction of combined parameters, such as decentering between core and ring, power shares of each component, as well as statistical measures like the variation of the ring width, of the ring diameter, and of the ring amplitude.

Measurement of a ring beam caustic following the measurement strategy with increased axial resolution. The z-positions of the feature focus (ff = 0.09 mm) and of the feature depth (fd = ff ± 0.35 mm) are indicated, much shorter than zR = 1.06 mm. The displayed intensity distributions at various axial positions illustrate the evolution of the beam shape along the propagation axis.

© Primes

Caustic Parameters for Ring Beams

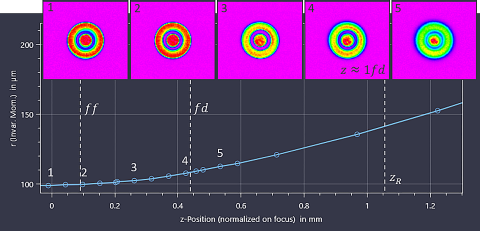
In caustic measurements, it is evident that traditional beam parameters—such as beam quality, Rayleigh length, or waist diameter—are either not meaningful or potentially misleading when applied to ring beams. Most importantly, the ring and core feature disintegrates within a fraction of a Rayleigh length. Consequently, there is a need for new parameters that accurately characterize the process-relevant caustic properties of these beams.

Starting from the beam waist, we analyze the propagation of the power density distribution along the beam axis. As previously described, the ring beam parameters are examined in individual measurement planes around the beam waist. The evolution of these parameters along the axis is then analyzed, resulting in the definition of two new caustic parameters: feature focus location and feature depth.

The feature focus location indicates the axial location where the respective dominant feature of the beam attains its minimum size (see “feature depth”). Due to optical misalignments or inhomogeneous fiber emission angles, the sharpest image of the ring feature may differ from the beam waist according to ISO 11146. The diameters of the core and ring at their respective feature focus location are referred to as the feature focus diameters.

The feature depth is analogous to the Rayleigh length for ring beams. It describes the axial distance over which the ring feature of the beam is maintained to a certain extent. According to ISO 11146, the Rayleigh length is defined as the distance at which the beam diameter increases by a factor of √2 relative to the waist. For ring beams, this concept is adapted to define the feature depth. While Gaussian beams are characterized by their beam diameter, we need to find another descriptive feature for ring beams. Plateau beams exhibit differing beam quality in the ring and the core: the core tends to lose its shape more rapidly than the ring. Conversely, in single-mode ring beams, this behavior is inverted, with the ring losing its shape more quickly than the core. The feature depth is thus defined as the shortest axial distance after which the width of either the ring or the core increases by √2, measured symmetrically around the feature focus location. Typically, the feature depth is significantly shorter than the Rayleigh length and provides a useful metric for process window optimization.

Given that the feature depth is considerably shorter than the Rayleigh length, a higher resolution in z is required—more than prescribed by ISO 11146. Specifically, at least five axial positions within one feature depth on either side of the feature focus should be measured. This allows for a clear separation of the ring and core regions, enabling a ring-beam-specific analysis.

Conclusion

This work demonstrates that conventional evaluation techniques are insufficient for a meaningful description of ring beams. The introduction of these new parameters provides an accurate, comparable and relevant characterization of ring beams both in the focal plane and across the full caustic. This framework lays the groundwork for discussions on establishing an ISO standard for ring beams.